Assessing the Quality of the Modelling of Continuous Variables in the 2D Domain – A Deterministic Approach
Background
Any quick search on Google on the subject of “Assessing the quality of models in the 2D domain” would provide tonnes of results, with a number of them referring to research papers proposing various ways to evaluate the quality of the output of a modelling process. The complexity of the theoretical approach described in these papers, however, is often the element which prevents the practical application of these assessment theories to our every-day workflows.
Evaluating the errors of our modelling effort has, nonetheless, practical advantages. Among them is the understanding of the quality of our models. Interpolation, i.e. the procedure of predicting the value of attributes at unsampled sites from measurements made at point locations (Burrough & McDonnel, 1998), is a typical example of a task in which the quantification of the errors of the predictions provide information not only on the quality of the choices we have made during the modelling process (in particular which algorithm and parameters to use), but also how well our models approximate the characteristics of our continuous variables.
Practical Assessment Methodology
At Exprodat we have often used a simple, practical assessment methodology which can be easily applied as the final, key step to a general interpolation workflow shown below.
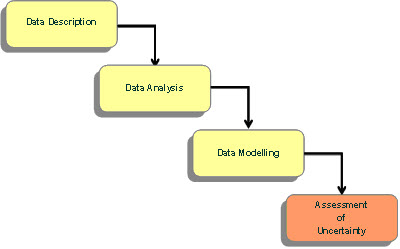
The methodology, tested and used widely to provide an understanding of the quality of the prediction of any continuous variable (in space, or time), is focused on a series of simple, easy to calculate parameters which can provide an insight on the performance of models.
Residuals are used as the key elements to evaluate the characteristics of the error population associated with the modelling effort. In particular, we look at two features of the residuals:
- their magnitude, both in term of absolute values as well as signed values
- their spatial distribution within the study area.
It is clear that in analysing the “fit-for-purpose” of the modelling process we have applied, not only are we interested in understanding how our models perform on average, but also where they provide more reliable results and whether there are patterns within the distribution of errors which can be recognised. The presence of patterns of high values of uncertainty could, for instance, be used to understand the ability of our models to predict values at the extreme of the distribution, an element that can be crucial in modelling workflows where the ability to model very high or very low values is of particular importance.
The Case for Investing Time in Evaluation of the Reliability of our Models
It may be argued that a model is just what it is: one of the possible interpretations of a complex reality, and in many cases we can get away with this. In this sense we may trust our results and consider that they are “reliable enough” for the purpose of our analysis. We do not need to go any further in our investigation.
On the other hand, what if we were able to measure the reliability of our models, so that we could pick the ones which are able to better portray the features of the continuous variables we are modelling? Wouldn’t we want to go that bit further and invest some time in evaluating the uncertainty if this could turn our modelling into informed-decision-making?
To be Continued….
This is the first of a three-part series of blogs on the subject of the “Assessing the Quality of the Modelling of Continuous Variables in the 2D Domain – A Deterministic Approach”.
In part 2 I will discuss some simple parameters that can be used to assess the quality of models generated from point datasets by using a deterministic approach to interpolation.
Posted by Paola Peroni, Senior Consultant, Exprodat.
Paola will be presenting elements of this methodology at the ESRI User Conference, Tue Jul 13th, 2010 (room 28 C), in San Diego.





